idetc2012c Presentation

Motivation

Understanding user preferences is a key to conceptual design, and has become practical through statistical learning.

Learning of the market has shifted from traditional questionnaires to more interactive, social-networked data.

How shall we create human-computer interactions to get data useful for design decision making?

The objective of this paper is to develop interactions that help to elicit preferred designs from the crowd.

carMesh: An interaction to elicit preferred cars

Please choose designs you prefer more and let the algorithm propose new designs.

Some rendering going on...Please wait

Generate better designs

Submit selected designs

Restart interaction

Related work to design preference elicitation

Conjoint analysis (CA): Learns preference model based on choice data; chooses queries adaptively to learn more efficiently.
Toubia, O.and Hauser, J.(2004), Toubia, O. et al.(2007), Netzer, O. et al.(2008) and others

Recommender systems (RS): Propose products based on the learned user profiles; Proposals can be improved by using crowd profiles (collaborative filtering).
Balabanovic, M. and Shoham, Y.(1997), Linden, G. et al.(2003), Adomavicius, G. and Tuzhilin, A. (2005), Das, A.S. et al.(2007) and others

CA focuses on modeling rather than finding the optimally preferred designs of users;
RS passively recommends existing products. It does not create designs to satisfy user desires.

Global Optimization: Optimizes a black-box function through statistical learning.
Jones, D.R. et al.(1998), Sasena, M.J. (2002) and others

Things to cover in this talk

Individual preference elicitation: Real-time learning from implicit feedback and design proposal mechanism

Improving elicitation through crowd interaction data

Elicitation using implicit feedback * Preference modeling using rankSVM
* Design proposal based on the modeled preference

Implicit feedback, or choice data, comparison data

A set of designs: $\{x_1, x_2, ..., x_n\}$

A comparison set: $\mathcal{I}$, for each pair $\{i_1, i_2\} \in \mathcal{I}$, we have design $i_1$ more preferred than design $i_2$.

Denote $\Phi(x)$ as unknown features of a design.

The preference is modeled as $f(x) = w^T\Phi(x)$. We call $w$ the user profile.

Preference modeling using rankSVM

Learn $w$ by balancing training error $\xi$ and model complexity $|w|$:

$\begin{eqnarray} & \underset{w,~\xi_{i_1i_2} ~\forall \{i_1,i_2\}\in \mathcal{I}}{\text{minimize}} & \quad \frac{1}{2}w^Tw + C \sum \xi_{i_1i_2}\\ & \text{subject to} & \quad w^T\left(\Phi(x_{i_1}) - \Phi(x_{i_2})\right)\geq 1 - \xi_{i_1i_2}, \quad \xi_{i_1i_2} \geq 0. \end{eqnarray}$

Let each row of $Z$ be a feature difference $\Phi(x_{i_1}) - \Phi(x_{i_2})$, the problem can be equivalently solved by its dual problem:

$\begin{equation} \underset{{\bf 0} \preceq \alpha \preceq C{\bf 1}}{\text{minimize}} \quad \frac{1}{2}\alpha^T ZZ^T \alpha - {\bf 1}^T\alpha \end{equation}$

A working-set selection algorithm (Fan et al. 2005) can be used to efficiently solve this QP; Kernel $K$ can replace $ZZ^T$ to implicitly define the feature mapping $\Phi$.

Solving this problem to get a preference model complying with the implicit feedback.

Design proposal based on the modeled preference

Balance of exploration and exploitation: Propose a design away from previous ones with high predicted preference value.

This is achieved by maximizing the merit function:

$f_{merit}(x) = \sum \alpha \left(\Phi(x_{i_1})-\Phi(x_{i_2})\right)^T\Phi(x) + b \min_i ||\Phi(x_i) - \Phi(x)||$,

where $b$ adjusts the importance of exploration.

A genetic algorithm is used to optimize the merit. A tradeoff exists between a better solution and a faster response to the user.

Learning from the crowd * A graph representation of crowd interaction data
* Better design proposal using the crowd graph * Simulation results

Crowd data

An individual interaction can be represented as a path.

A collection of individual interactions can be represented as a graph.
$\bar{p}_i$ is the average number of iterations to get to $i$th leaf vertex.

Use collaborative filtering to find similar users from the crowd

At some iteration $s$ in a new interaction, we estimate the user profile $w_s$ and find similar previous user profiles using

$f_{similarity}(w_s,w_{s\tau}) = w_s^Tw_{s\tau}/||w_s||||w_{s\tau}||$

Denote as $\mathcal{X}_s$ the set of most-preferred designs from previous users with the highest similarity to $w_s$. A heuristic proposal is to "jump" to one design in $\mathcal{X}_s$. But which one?

Heuristic proposal algorithms

JUMP1: Pick the most costly design, i.e., the one with maximum average cost.

JUMP2: Pick a design with minimum extra cost when the "jump" fails.

Let $\mathcal{X}_i$ be a set of leaf vertices that are descendants of the $i$th element of $\mathcal{X}_s$. Let $\tilde{p}_i$ be the average cost when we choose to query $x_i \in \mathcal{X}_s$ but it is not the optimally-preferred design for the user:

$\begin{equation} \tilde{p}_i = \frac{1}{|\mathcal{X}_i|}\sum_{j=1}^{|\mathcal{X}_i|} \bar{p}_{i_j}, \end{equation}$

Simulation tests set-up

We use simulations to show that both JUMP1 and JUMP2 improve the optimization efficiency.
1000 optimizations are solved in a sequence. Each has an optimal solution uniformly realized from the grey grids. All grids are candidate designs to be proposed.

Objective functions are modeled to be Gaussian.

The same initial guess (top-right and bottom-left pair) is used for all optimizations. Each new proposal contains one solution; each feeback contains one pairwise comparison.

The crowd graph and leaf costs are updated after each optimization is done.

Simulation results

Crowd knowledge can improve the optimization; JUMP2 has better performance than JUMP1.

JUMP2 converges to an almost fixed strategy while JUMP1 does not.

Initial guess updates

Update the initial guess to the optimal solutions obtained most frequently.

Fixed JUMP3: Update after every 200 optimization tasks. Drawback: Once updated, previous search data will be obsolete.

Adaptive JUMP3: Check if the current initial guess can represent the observed clusters of optimal solutions. If not, replace with the current cluster centers.

Simulation results

Adaptively update initial guess can further improve the optimization performance based on JUMP2.

Conclusions

The question "What designs do you prefer?" can be answered by the crowd through interactions with learning capability.

This paper demonstrated one potential interaction scheme and explained the underlying elicitation algorithms.

Simulation studies showed that crowd interactions can improve the efficiency of future elicitations.

Future work

Real-user tests will be conducted to evaluate the proposed heuristics.

Structured design representations will be used to enrich design variation. Learning methods on structued data (as oppose to vectorial one) will be investigated.

Evolutionary algoirthms on structures will be used for design proposal. Figure from Karl Sims' work on evolutionary creature. Sims (1994)

Acknowledgement

The authors would like to thank Professor Richard Gonzalez, Professor Clayton Scott and Professor Honglak Lee for their valuable input to this work.

carMesh is created based on the feedback from: Alex Burnap, Steven Hoffenson, Kwangjae Lee, Soodeh Montazeri and many others.

presentation available at http://maxyiren.appspot.com/idetc2012c.html Thank you all for attending.
What questions do you have?

Research Fellow
Optimal Design Lab
University of Michigan
yiren@umich.edu
maxyiren.appspot.com

Professor
Optimal Design Lab
University of Michigan
pyp@umich.edu
ode.engin.umich.edu

Kernel implementation in carMesh

$x$ are distances between control points.

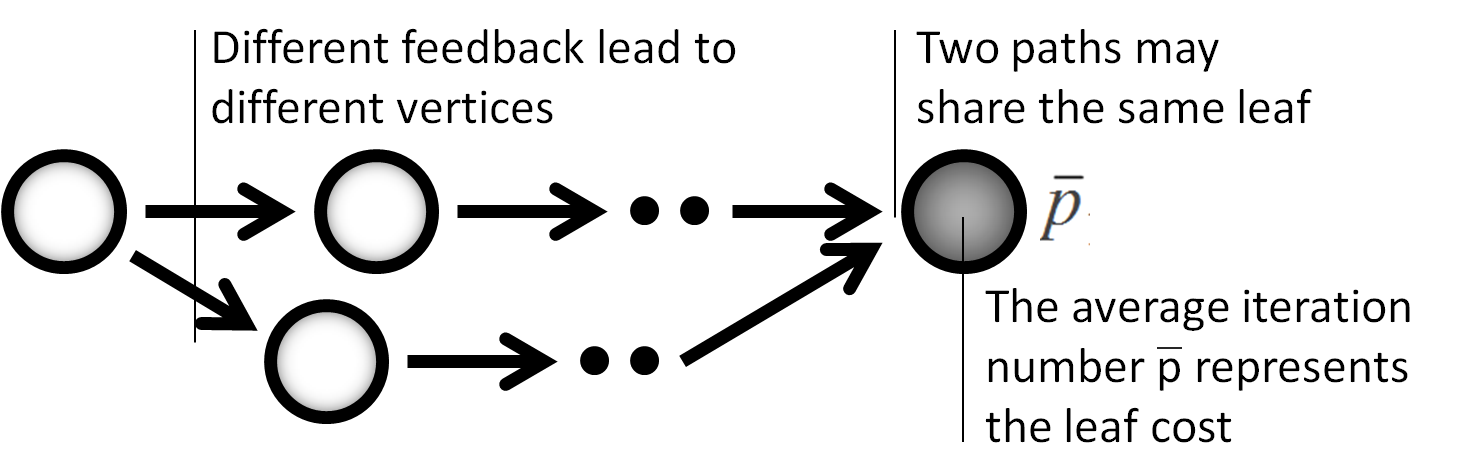
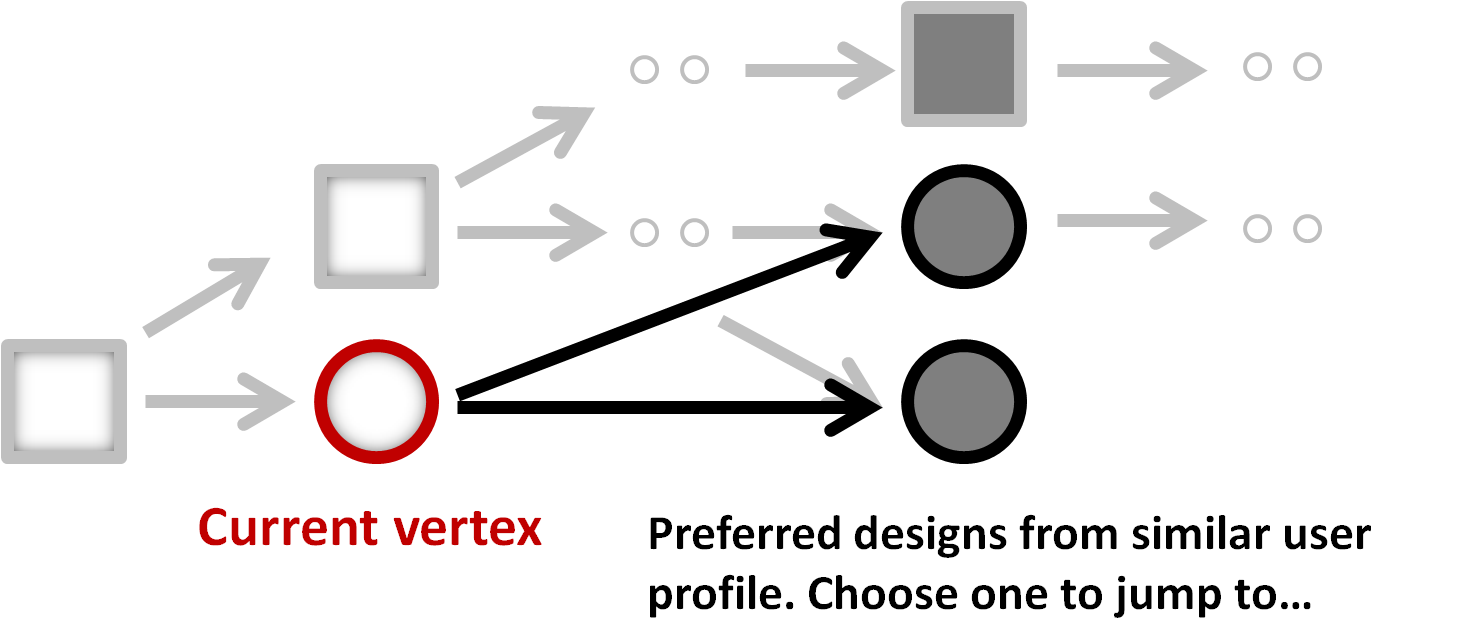
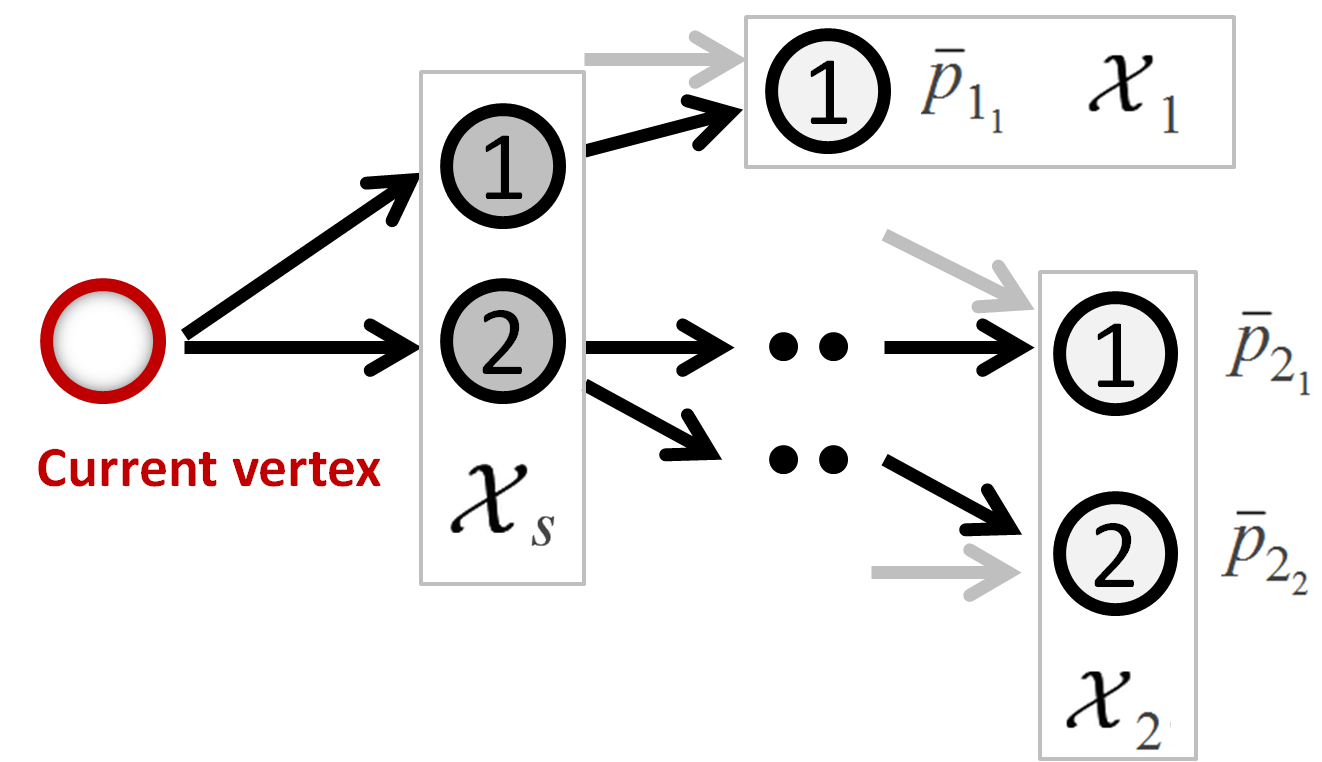
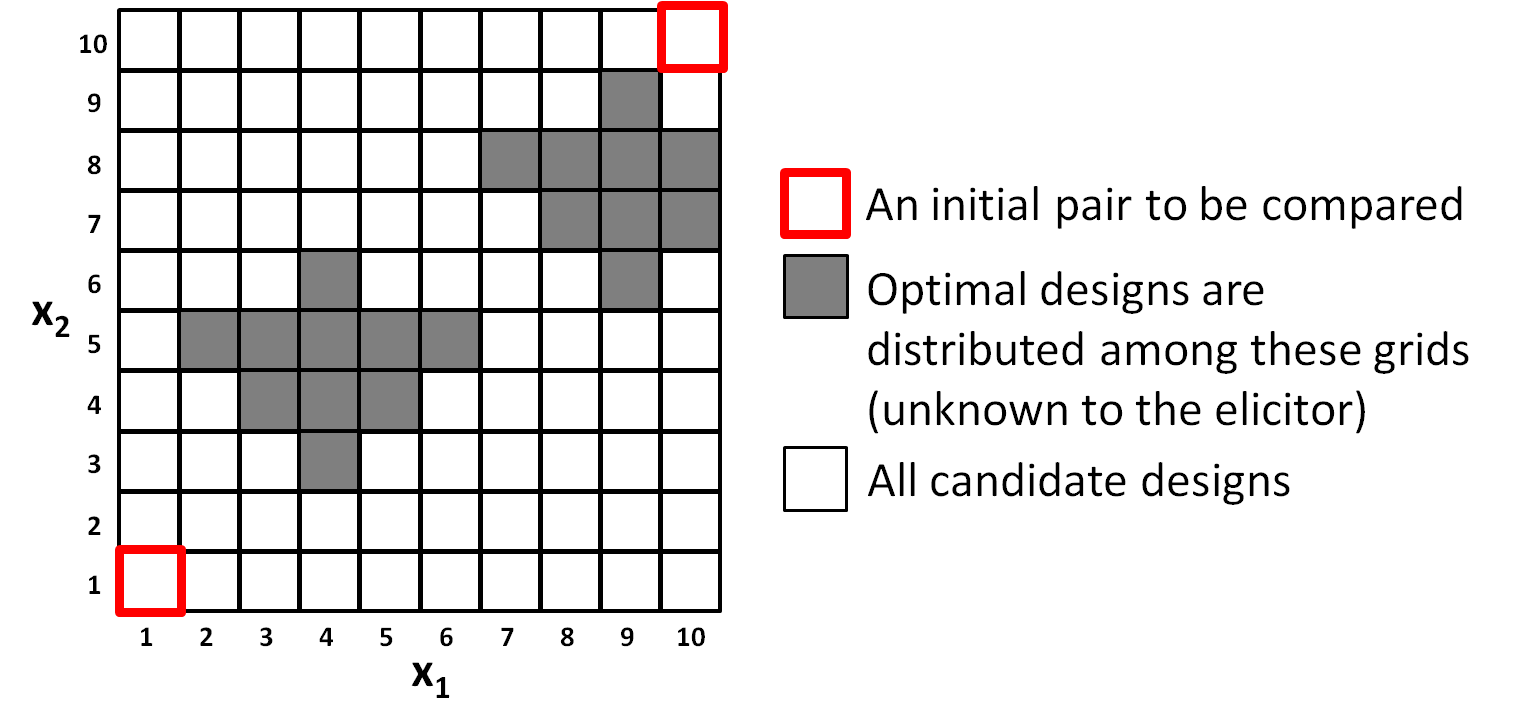
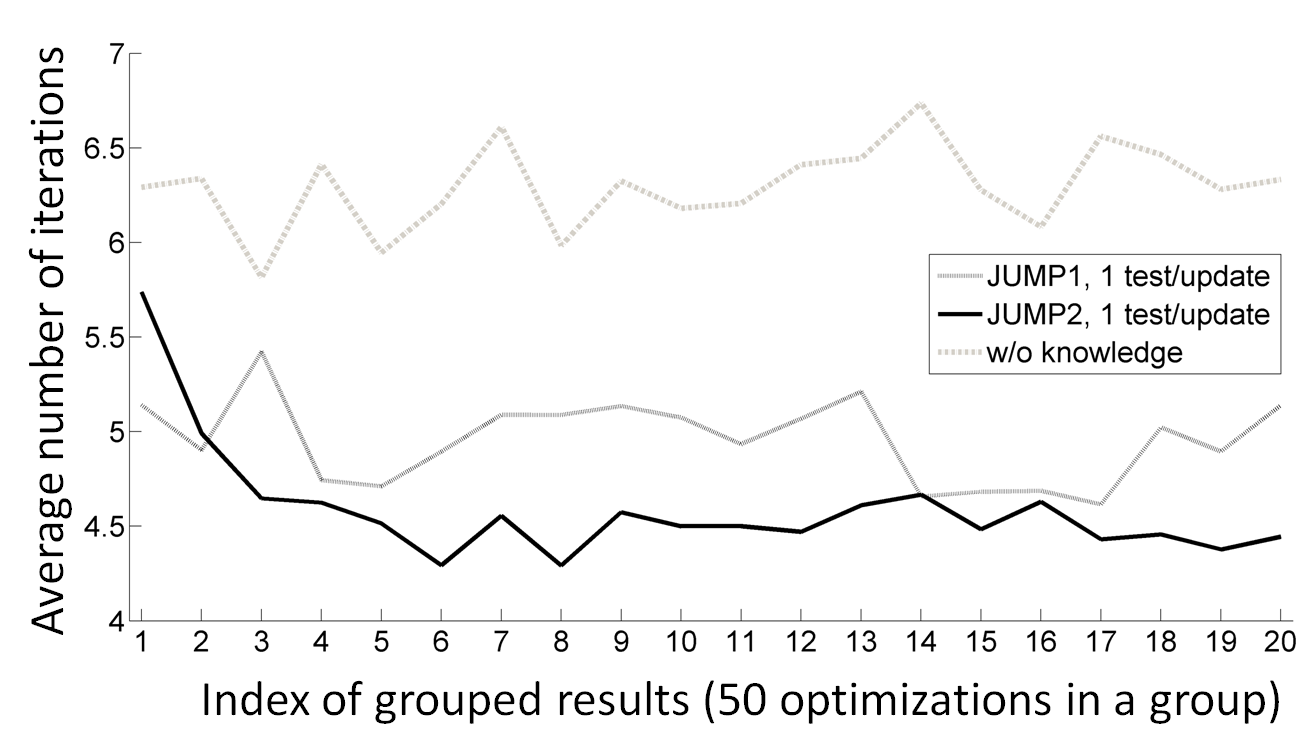
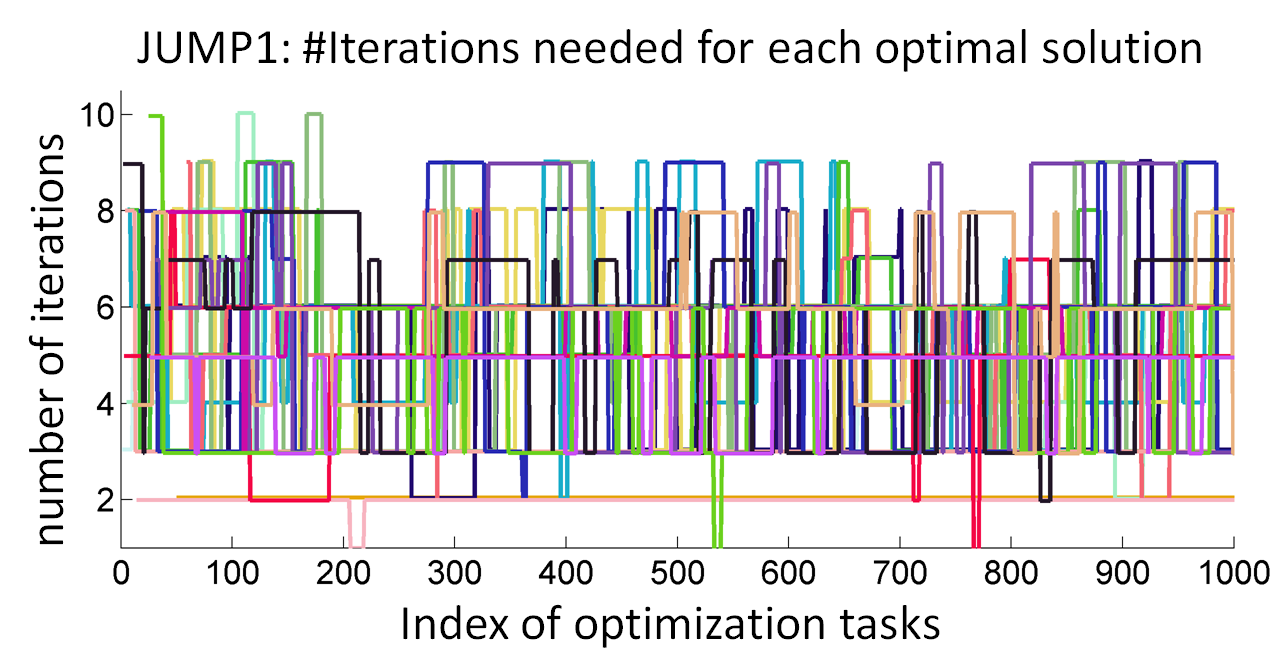
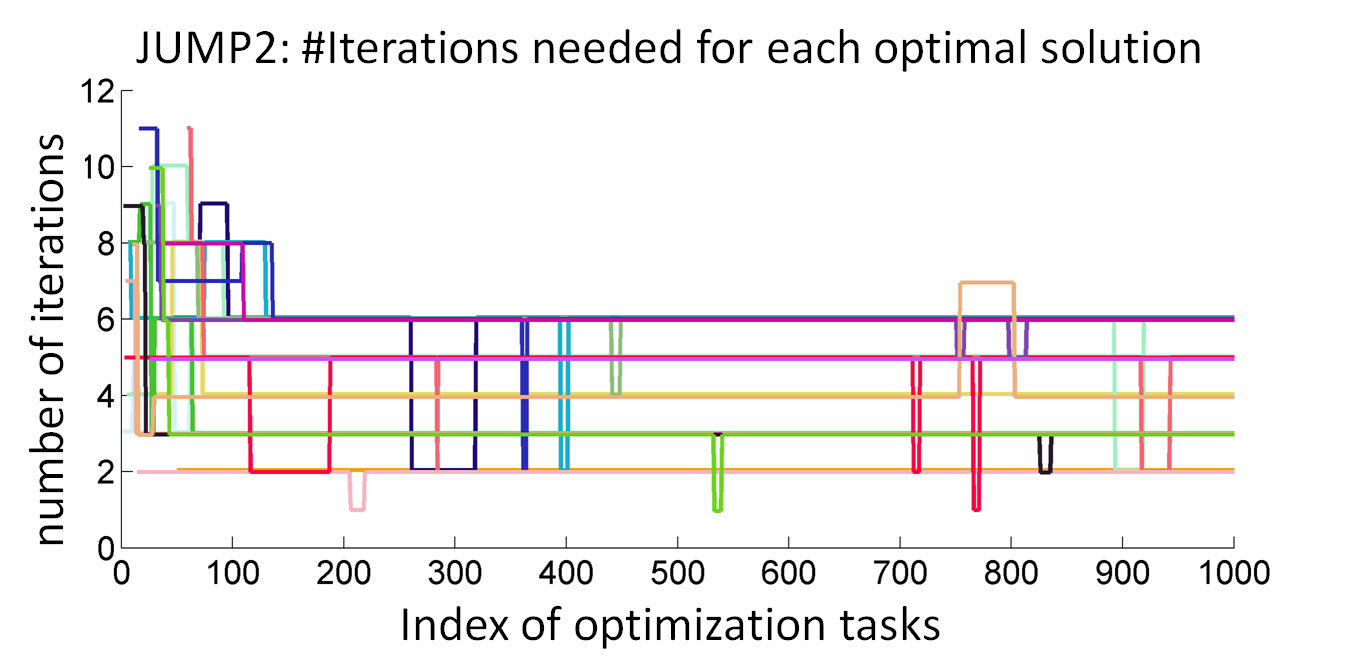
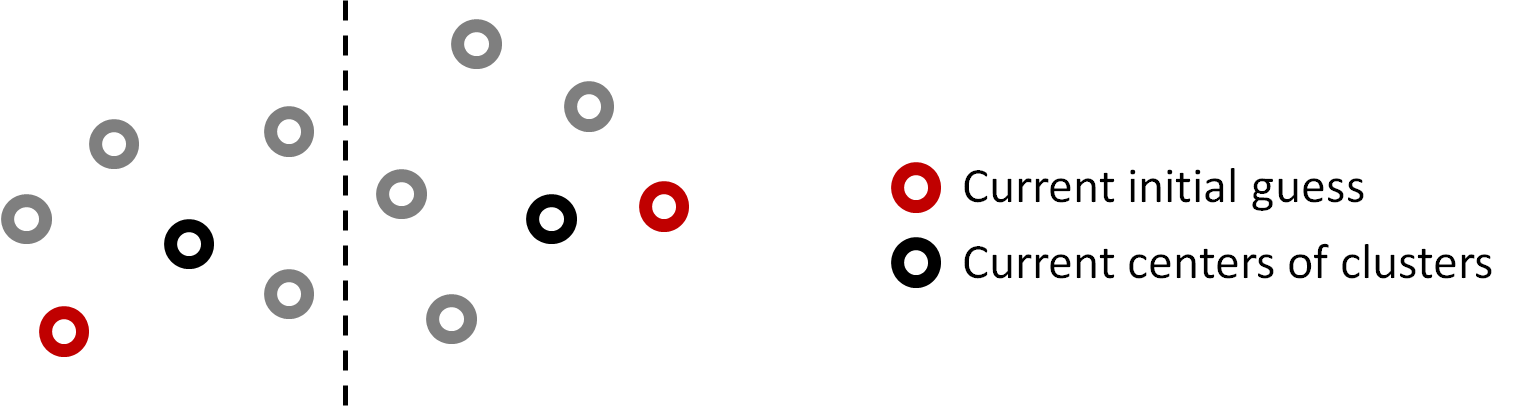
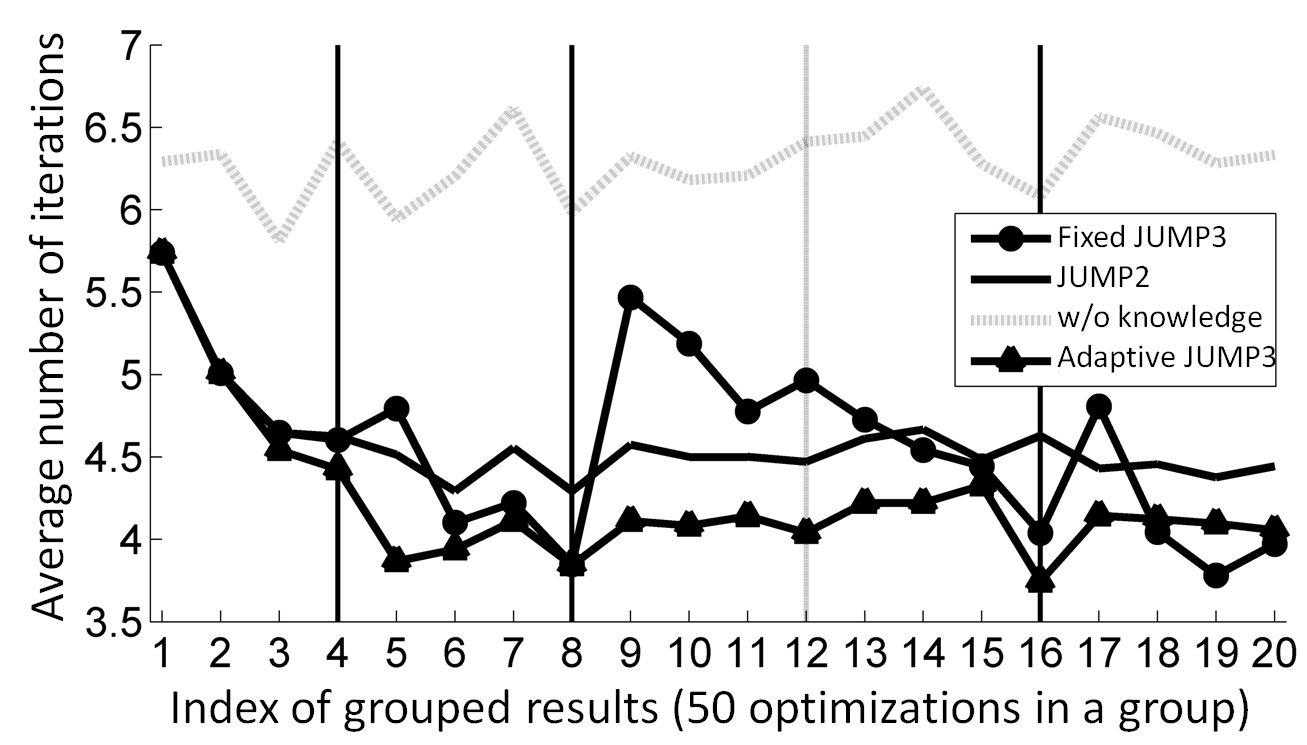
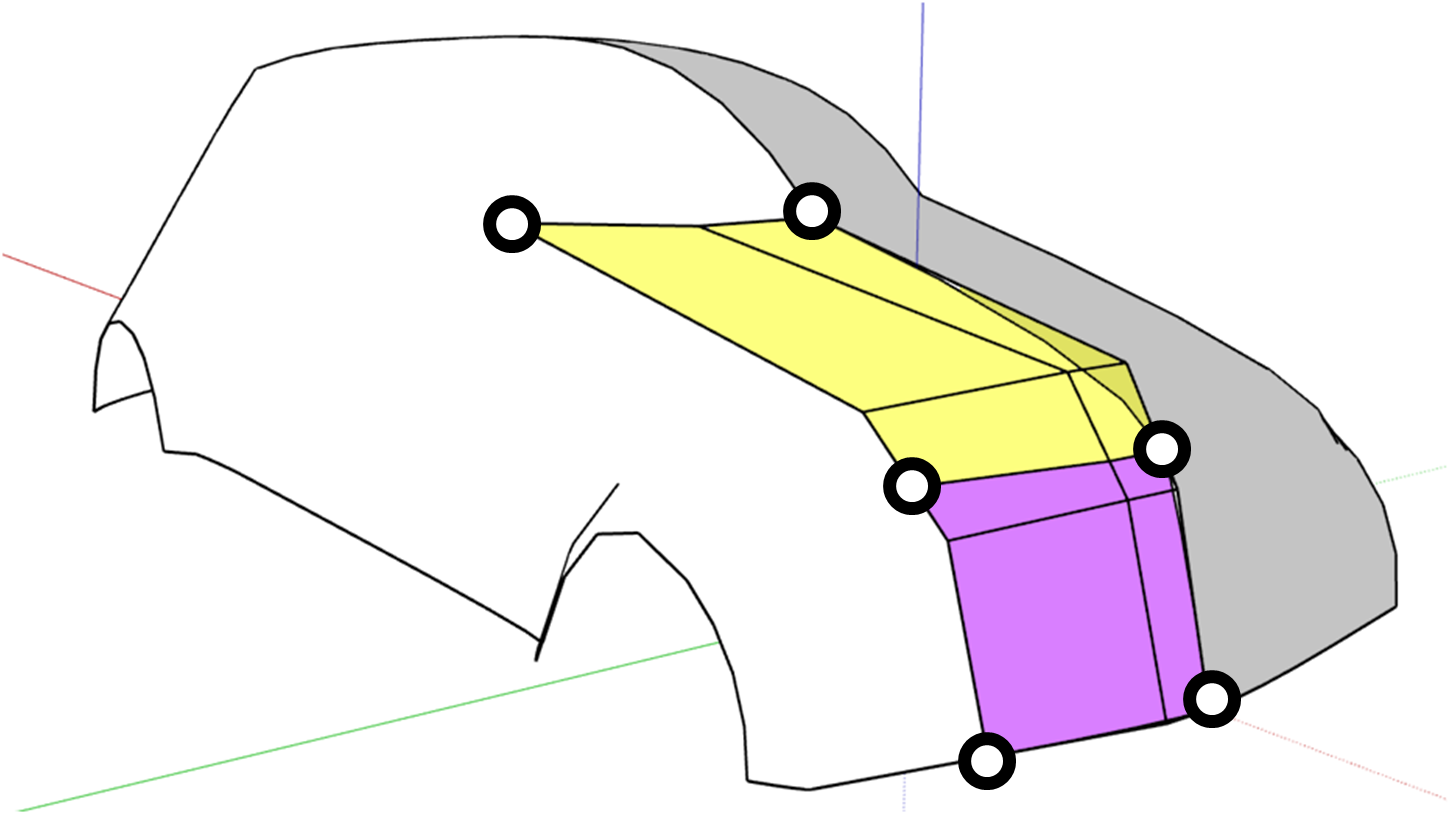
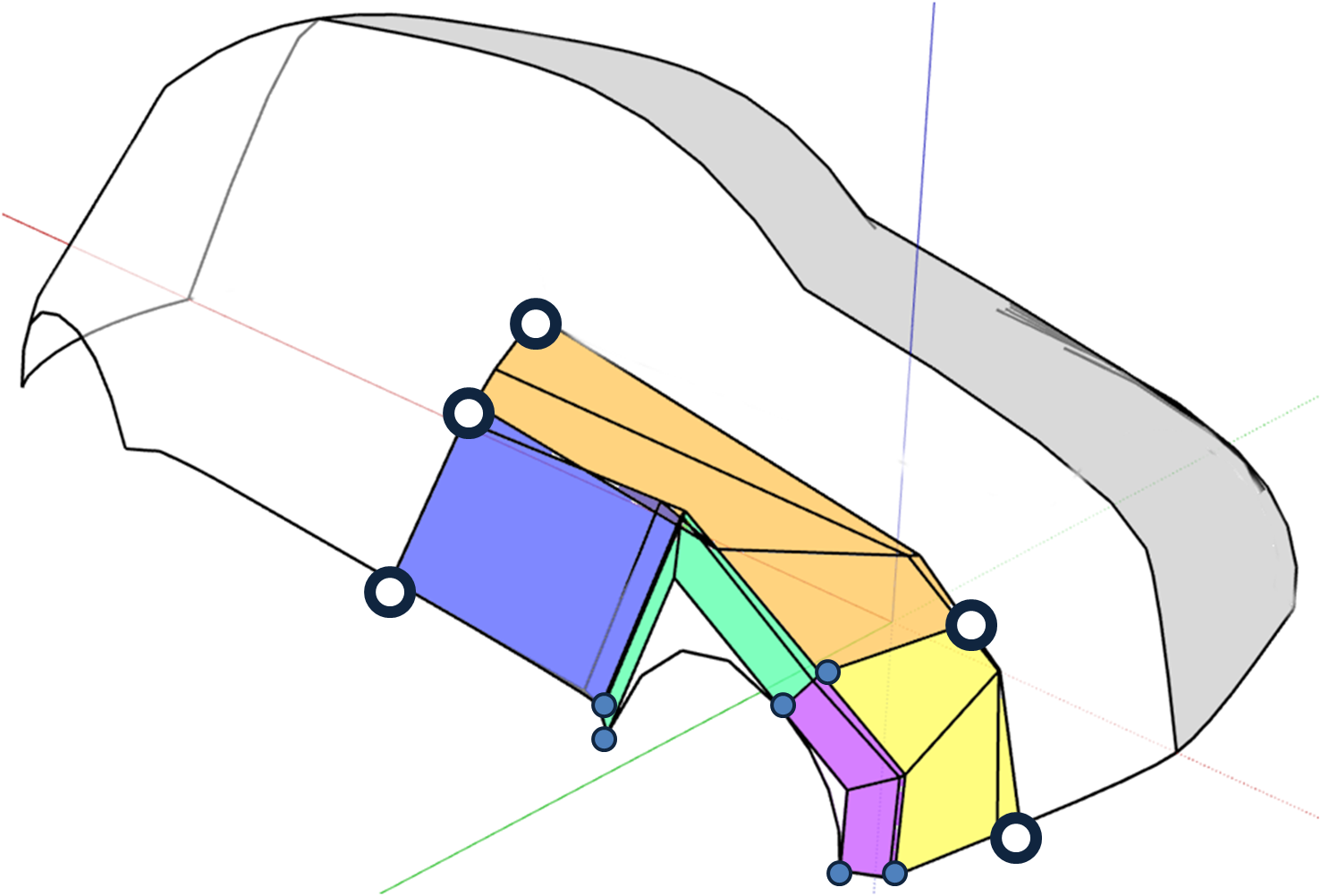
An RBF kernel is used to measure the similarity between two design differences:

$\begin{eqnarray} K_{ij} && = \left\langle \Phi(x_{i_{1}})-\Phi(x_{i_{2}}),\Phi(x_{j_{1}})-\Phi(x_{j_{2}})\right\rangle\\ && =k(x_{i_{1}},x_{j_{1}})+k(x_{i_{2}},x_{j_{2}})-k(x_{i_{1}},x_{j_{2}})-k(x_{i_{2}},x_{j_{1}}), \end{eqnarray}$

where $k(x_i,x_j) = \exp(-||x_i-x_j||^2/p)$ and $p$ is the dimensionality of $x$.